Judgments

All statements, when evaluated in a logical context, result in a judgment. This judgment can only ever be one of two values: affirmed, or denied. This would be called a "truth value" in our universe, being either true or false.

Negation

"If a short vertical stroke is attached below the content stroke, this will express the circumstance that the content does not take place." This can be prepended to almost any statement to invert its judgment. It is exactly equivalent to using a "!" operator.

All of the following would evaluate to affirmed:

Letters

Letters, to quote Frege, are used to "understand different objects" and "serve chiefly to express generality." That is, in our terms, they are variables. Following the original paper, all letters are (obviously) a single character in length, and they are always displayed in a German Fraktur typeface.

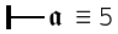
Letters are asserted using the judgment stroke which precedes them. An initial value must be given. If that value is affirmed or denied, only the judgment stroke (plus appropriate negation stroke) will be displayed.

Generalities

More commonly known as a universal quantifier, these are pretty similar to a for loop in programming. There is an important difference, however, in that unlike for loops they are universal. They iterate over every possible value. It isn't very often that one needs to iterate over every integer! Therefore in Gottlob the generalities are strictly particular. Given a letter, the generality will loop from 1 up to the value of that letter. If given a matrix of values, it will assume every value in that matrix. Within the body of the generality, the letter receives the current loop value, but it retains its original value everywhere else.

In the following example, the loop would print out [3,6,9,12,15] and then the next line after the loop would print out 5.

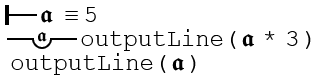
Generalities are still logical operators however -- the value which is returned in the end is only affirmed if each and every iteration evaluates to affirmed. This means that in addition to for loops, generalities can also be used to apply a test to many elements at once. The following example will go through all the values in the matrix and test if each is evenly divisble by 2. As several of them are not, the judgement on the entire generality is denied, and that is what would be printed out to the program console from the following statement.

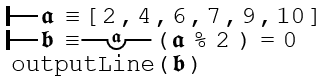
Matrix generalities

This is a new extension not found in Frege's work, but it felt true to the source material and proved to be very useful for real programming. It operates the same way as the normal generality, except that the results from each iteration are accumulated in a matrix which is returned as the result of the entire operation. The following example multiplies every element in the array by 5. A new matrix containing these results is returned and saved in 𝖇. The last command print it out to the console: [25,35,60,75].

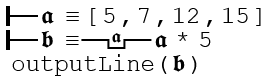
Conditionality

Conditionality is the basic logical operation in Gottlob, but like generalities it serves double duty as it can also be used as an if statement.

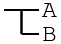
Note, however, that we are talking about logical implication here. B → A is only ever false if B is false but A is true. In the context of Gottlob, that means that if the test (B) of an implication is denied, then the consequent (A) is never executed -- yet the value of the entire expression if affirmed! For anyone with a programming background, it is probably safest to think of implication in its logically equivalent form of !B || A to avoid confusion.

As conditionality is the only logical operator aside from negation, one must get a bit creative in their use. The logical equivalent to (B && A) → C is simply a nested set of implications: "If B then (if A then C)." If this was in the context of a conditional, then C would be code that should only be run if both B and A are affirmed.

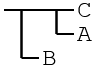
(B || A) → C can also be formed with the application of the !B || A rule. By negating the one side it becomes a simple or statement. "If (if not B implies A) implies C." Again, in this example C would be code that should only be executed if either B or A are affirmed.

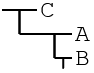
Conditionals don't have to be used as if statements, however. If you only want to create a judgment, that can be done similarly. B || A is the equivalent of !B → A or:

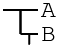
Likewise B && A is the equivalent of !(B → !A) or:

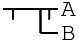
All of these and more can be derived from the !B || A rule, but by this point it might be clear why programmers in our timeline moved away from implication as the primary logical operator. See the Frege paper for even more extreme examples!

Expressions

These are any standard programming language expression. They are, for simplicity's sake, entered as the equivalent Javascript. Don't worry about trying to type in Fraktur or Greek or using the fancy names for true/false, that will all be taken care of automatically. Entering "(a-17)%12<=7" will result in the following:

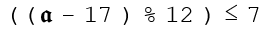
While "phi(true)" will give you this:

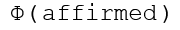
Assignment

This is exactly like when a letter judgment is added, except without the judgment stroke. This is a slight departure from Frege, who said, "we must insist that throughout a given context the letter retain the meaning once given to it." That would be rather impractical for a working programming language, so the meaning of letters can be changed. Assignments can be explicitly inserted from the editor tools, or they can be added in Javascript as part of an expression, it all results in the same syntax tree.

Judgment

The judgment stroke can be prepended to any statement. If this is done, that statement return value must be affirmed, or else the program ends immediately. (A negation stroke can be added to ensure that the statement is denied, of course.) This feature can be used as the kind of assert statement found in many languages from our universe. The following guarantees that all members of i are less than 5, for instance.

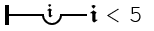
Bracketed statements

Not everything in Gottlob is limited to a single line. The body of generalities, the consequent of conditionalities and the body of functions can all contain multiple lines of code. In generalities and conditionalities these will be rendered as being contained within square brackets, following the examples in Frege's work. In both of those cases, the judgment on the entire block will only be in the affirmative if the judgment on each individual line is affirmed.

This generality will only be affirmed if every member of 𝖆 is between -17 and 20.

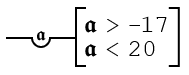
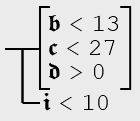
While this conditionality will only be affirmed in the situation when, if 𝖎 is less than 10, then all of the following are also affirmed: 𝖇 < 13, 𝖈 < 27 and 𝖉 > 0.

Matrices

Gottlob has support for matrices (i.e., arrays). These can be declared as literals where a=[1,1,2,3,5,8,13] would give you:

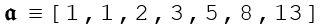
Matrices as rendered are indexed from 1, to pay respect to their mathematical origins. Other than that, you use standard Javascript notation when entering matrix references in expressions like a[1][2] to get the second element of the first element of 𝖆. That will be displayed in a more "mathy" version using subscripts:

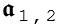
The subscripts can be arbitrarily complex. (Though, to be perfectly honest, this has been a recent source of bugs...) Entering b[m*2][n[7]]=f[f[f[13]]] produces the following:

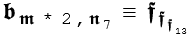
Functions

Functions work more or less as you would expect, since that notation was established long before Frege. The value of the final line is used as the return value. Functions are all listed at the bottom of the program, regardless of when they were declared. If you give them the name of a Greek letter, it will always be rendered using that letter. This is the encouraged best practice, as it is most faithful to the original material, but it is not enforced.

The following example asks for a number from the user. This is passed to the function Φ(𝖆) which first checks if 𝖆 is negative. If so, it adds 27 to it. The last line multiples the new value of 𝖆 by 5. Because this is the final line of the function, that's the value that gets returned and is printed out to the console. Thus if the user enters 10, the result is 50, but if they enter -30, the result is -15.

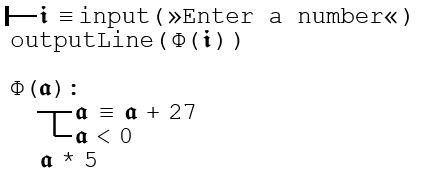
Several utility functions are included for your convenience. These do not use Greek letter names, as that wouldn't leave very many available for user programs.

output(x)	Prints x to the program console.
outputLine(x)	Prints x to the program console, followed by a newline.
input(x)	Prints x to the program console, then reads in input from the user which is returned.
cls()	Clears the console.
abs(x)	Returns the absolute value of x.
len(x)	Returns the length of x, if it is a matrix.
push(x, y)	Pushes y onto x, if it is a matrix.
pop(x)	Removes the last value of x and returns it, if it is a matrix.
unshift(x, y)	Adds y onto the beginning of x, if it is a matrix.
shift(x)	Removes the first value of x and returns it, if it is a matrix.