The Begriffsschrift describes three basic operations: conditionality, negation and generality. Later in the work these are used to define other operations, as part of the series of proofs that Frege developes. While interesting in their own right, they don't have any obvious application to a programming language and are not used here.
Whenever possible Frege's own words will be used to describe these operations. All emphasis is in the (translation of the) original.
Conditionality
"If A and B stand for contents that can become judgments, there are the following four possibilites:
(1) A is affirmed and B is affirmed.
(2) A is affirmed and B is denied.
(3) A is denied and B is affirmed.
(4) A is denied and B is denied.
Now
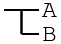
stands for the judgment that the third of these possibilities does not take place, but one of the three others does."
In modern notation this would be written as B→A, B⊃A, "B implies A" or even "if B then A". If you're not familiar with the implication operator, the tricky thing to remember is that if B if false, the truth value of the operation is always true. That is, a false statement logically implies everything. Consider the statement "if it is raining, then I am wet". It only deals with situation where it is raining, in which case I must be wet for the statement to be true. If it isn't raining, however, it has nothing to say. Maybe I'm dry, and maybe someone just dumped a bucket over my head. In either case the original statement is still true. For those coming from a programming background, it is probably safest to think of this as its logical equivalent !B || A.
Negation
"If a short vertical stroke is attached below the content stroke, this will express the circumstance that the content does not take place. So, for example,
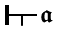
means '𝖆 does not take place'. I call this short vertical stroke the negation stroke."
This works like any other negation operator, and there isn't much to say about it. It is the same as '!' and can be used in all the same places.
Generality
"In the expression of a judgment we can always regard the combination of signs to the right ofas a function of one of the signs occurring in it. If we replace the argument by a German letter and if in the content stroke we introduce a concavity with this German letter in it, as in
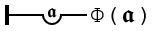
this stands for the judgment that, whatever we may take for its argument, the function is a fact."
This is now called a universal quantifier, using the ∀ notation, but the core idea hasn't changed any.
These are nothing more than the standard tools of Aristotelean syllogisms given a more formal presentation. "All people are mortal" can easily be encoded using these tools. In modern notation it would be something like:
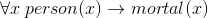
While using Frege's notation it would be the following:

If you are familar with first-order logic you may be expecting an existential quantifier to allow statements like "a person exists".
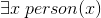
However, like many of the early systems, Frege did not bother to provide a separate existential quantifier. It isn't strictly needed, as one can always be created by combing generality with the negation stroke:
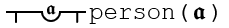
"It is not true that for all 𝖆, 𝖆 is not a person", i.e., "there exists at least one 𝖆 which is a person".